For the hallucination room, I attempted to create an installation playing on the invisible systems which we embed cognitively. Orbital systems and their paradoxical relationship to systems of a disruptive cognitive nature could change our perception of reality. Largely, I am fascinated by the axiomatic design of non-Euclidean geometry and, if due to this, human beings could begin to optically and cognitively perceive non Euclidean geometry whilst living in a perceptually valid Euclidean world. Also how this would affect people’s theory of mind, experience of narrative, and spatial/ temporal space perception. I attempted to let people subliminally play with a hallucination that may speak to an unknown or unperceived reality. This attempt was largely ineffective, though it gives better structure and ideas for future explorations.
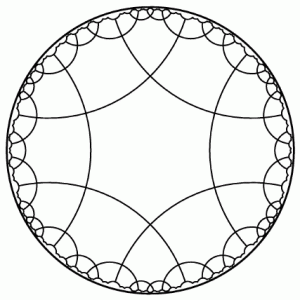
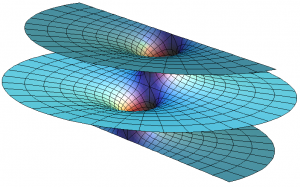
To begin, a simple explanation regarding the definition of non-Euclidean geometry: In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to Euclidean geometry. Non- Euclidean geometry arose historically due to the logical invalidity of Euclid’s fifth postulate. Euclid’s fifth postulate stated that two parallel lines will eventually meet, which was found to be invalid: thus non-Euclidean geometry was born. Non-Euclidean geometry “arises when either the metric requirement is relaxed, or the parallel postulate is replaced with an alternative one.” With the replacement of Euclid’s fifth parallel postulate, one obtains either hyperbolic and elliptic (riemannian) geometry. The essential difference between Euclidean (the geometry that we see/ perceive) and non-Euclidean (what we cannot) is the fifth postulate, more commonly known as the parallel postulate. So, in Euclidean geometry, lines are at a constant distance from each other and are known as parallel, two points will equal a line, and is the geometry learned in high school and the geometry of our perceived world. Non-Euclidean geometry, simply speaking, is not that- and comes to two well known non-Euclidean geometries: Hyperbolic and Riemannian. Hyperbolic plane geometry replaces the fifth postulate of Euclidean geometry with its own. Hyperbolic plane geometry is known as the geometry of saddle surfaces or pseudospherical surfaces, meaning, surfaces with a constant negative Gaussian curvature (a saddle shape). Some physicists, in the likes of Einstein, believe that space is curved and that the general theory of relativity adheres to hyperbolic geometry. This has been recently disputed as evidence has actually pointed to more flat based geometry, though it is still under investigation. M.C. Escher utilized hyperbolic geometry in a lot of his work. In Riemannian geometry (sometimes known as elliptic geometry or spherical geometry) the lines curve forward. Riemannian is the geometry of curved surfaces- which is directly connected to our lives on our curved surface, Earth. Non-Euclidean geometries are those that we do not easily perceive, but are forces that mysteriously shape our world, and that nonetheless live in logical and axiomatic truth.
Graphic Examples: From left to right: A Hyperbolic Sphere, a naturally occurring hyperbolic sphere: Coral, M.C. Escher’s usage of non-Euclidean geometry, a Riemannian surface.
Authors such as Borges and Dostoevsky utilized non-euclidean geometry and the way it plays with temporary spatial perception to be used as a catalyst and subject in their narratives. They also utilized the narrative structure in which non-euclidean geometry was born out of: Axiomatic systems. Borges utilizes the structure of an axiomatic system to go through The Library of Babel, in which the narrative architecture is Non Euclidean. Borges essentially subversively manipulates his audience and brings them into his world through the use of an axiomatic system, which is inherently designed to be logically valid to human beings. Thus, further deepening the validity, investment, and intrigue in Borge’s audience has in the story. Subversively, Borges utilized the subliminal way that our brain plays with the validity of logical, axiomatic thinking in order to facilitate a great spatial understanding of the space. Borges made the brian play with itself. Some may think this is hallucinatory and, frankly, evil.
In The Brothers Karamazov, Dostoevsky used the axiomatic system of Non Euclidean geometry to show how it could disrupt natural systems, i.e. God’s creation, thus theologically rendering non euclidean geometry similar to evil. This is also a factor in why I chose this topic for this project. One of the main characters of the book, Ivan, contends that non euclidean geometry should not have been made if there was an all knowing, perfect God. Because, if there was such a God, non-Euclidean geometry should not have been allowed to exist. Non euclidean geometry was a mathematical discovery, one based in reason, whereas the firm belief in euclidean geometry was a belief in reason- but now reason states, that is wrong. This is similar to how evil relates to Godliness- we are told that evil is necessary/ that God created evil, though this makes no sense and causes doubts in many believers. Yet, it is called reason and systematically validated. Ivan fears insanity as his beliefs in reason and God are shaken when confronted with the invisible system of non-Euclidean geometry.
Mitch Stokes in “Dostoevsky on the problems of Evil and Geometry” expands further:
“ Ivan’s struggle mirrors the West’s. Since before Plato, the West held reason in high esteem (The modernist spirit is not, therefore, modern after all.) But then – just when the Enlightenment was hitting its stride- reason threw itself into doubt with non-Euclidean geometry. This discovery is one of the main causes of postmodernism’s suspicion of reason. But much of Dostoyevsky’s commentary here would be lost on us without an appreciation of the non-Euclidean revolution. And this is but one example of how widespread mathematics influence is. Not putting too fine a point on it, mathematics is important. But merely being able to do mathematics is insufficient, primarily because there’s much more to understanding mathematics than recipes and formulas. To be sure, mathematics is a powerful means for describing, predicting, and controlling the physical world. But its study is also required for understanding culture. To allude to Kant: calculation without understanding is empty, understanding without calculation is impossible. Our problem with geometry is not the modernist’s; our problem is that we don’t understand it.”
Various illustrations of the library of Babel
I wanted to further allude to this problem in my design and how non Euclidean geometry represents an important function of human culture in general. The functions, restraints and study of Non Euclidean geometry is similar in how human beings embed hierarchical power structures and give them episodic validity, thus making them ‘real’ and able to initiate action. This alludes to how such episodic validity is given to other structures of power such as a belief in capitalism, white supremacy, etc. The mystery behind such immense belief is often puzzling and in direct adherence with the quote alluding to Kant via Stokes “calculation without understanding is empty, understanding without calculation is impossible.” This is a topic I wanted to explore along with this phenomenons interactivity with culture.
Rigorous axiomatic systems in which non Euclidean geometry are built on are similar to how neural structures work in the brain, in that they are validated systematically and repeatedly through different conceptions of “proof”. When viewing a space, our brain is calculating temporally and mapping spatially- which is calculation. But, one must need understanding and moreover, ecologic validation. Understanding comes from the negotiation with context, object, function, and form. An installation is the perfect venue in which to have this negotiating playing in real time. While using this logical mode of thought, and in an attempt to make non euclidean structures neurologically valid in terms of spatial acceptance, I tried to facilitate such understanding through using materials and forms that allude to natural systems fixed with the juxtaposition of such non Euclidean traits via mapped projections, which were reliant on light.
Paradoxical Design: Intention and Failure
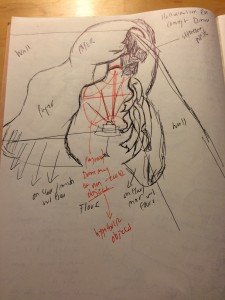
My installation was informed by physical materials symbolizing natural systems, which I used to structure my installation. I built the idea of my surface around natural systems. Utilizing the materials of paper and plastic, I was able to build using said natural systems in the most common way we consume them- in their condensed, commodified, capital form. A similar sizing down to the singular model and example of a system of Non Euclidean geometry I used in clip form.
My original plan for the structure of this project was to further build out the space with pieces of hard construction paper and have the projector inside the structure- thus the natural system would be housing the “un natural”. Though, this did not work out
Originally, the structure was supposed to be made entirely out of paper, but that changed as I began experimenting with plastic, canvas, and a hard white styrofoam. I played with many alternate materials. I enjoyed working with the paper material, canvas, styrofoam and plastic for the natural systems form and materials. The physical structure worked semi-well. It definitely gave the mood of a natural system, though the paradox effect did not come off generally.

The hallucination attempted to be the result of the strange merging and acceptance of two seemingly juxtaposed systems- of the physical structure/ material and of the material of light from the projections. In the installation, it ended up looking like they did not interact due to the structures not correctly harnessing/ manipulating light. I wanted the non-Euclidean structure to be represented through light- as light is another things which humans perceive but do not necessarily consider the systems behind. (I.e. how such invisible systems are living underneath common acceptance and how that is brought to life through the juxtaposing materials.) Similarly, the juxtaposition between the light of the projection and the materials was almost too extreme for effectiveness. The scene looked cluttered and was not as intended. It was not captivating enough for people to look at or even mildly be interested at interacting with, as the narrative of an unidentified model, colors, and structure were not enough to inform even a mild narrative. This was definitely a good learning process for me.
This installation was not successful as the light did not interact with the physical structures as thought. Even with this fact, it was similar to my original intention of the piece. Such invisible systems contrast- with the natural, preconceived, and perceived areas of it. Due to my preconceived notion of non Euclidean geometry during construction, the perceived areas did not have such an alarming effect for the general audience due to their extreme juxtaposition, but if looking closer, the paradoxes still ring true. There is still the perception of illusion for the audience within the work.
For instance, looking up close on the paper object, it became clear that the digital fabric was juxtaposing with the material as well as interacting with it. The merging of these two materials: paper and light, created a paradoxical, juxtaposed effect, though still seemed to merge. This is similar to how I hypothesize humans could begin to interpret non Euclidean geometry. Though, that was not clear or present to the audience or to anyone if they were not actively interacting with the installation- which my choice of structure and clips did not allow.



The clips also worked well, though they were not nearly dynamic enough to engage an audience whatsoever. I understood that the way to play between this juxtaposition was to rely on simpler clips that allowed for the space to negotiate itself- such as the single clip of the Non Euclidean model animation. The positioning of the projector, paired with this clip, allowed for the light to look as if it were pulling the materials into its enclosed reality. I learned that with the negotiation of context, simplicity is key as well as focusing on playing with light.
I arrived at my map by looking at a behavior that requires our utilization, understanding, and commodification of it: a systematized investigation of a system we view as natural. For this, I began wondering about how humans use water- to drink, to bathe, to relax. Creating another system from the natural system that is the creation and use of water. Similar to Euclidean geometry, we see this as normal and non disruptive. I disrupted this by taking footage of people using water and reversing it and flipping them to have a paradoxical effect. Over this I projected various Non-Euclidean models, each representing themselves on the basis of great circles. I mapped this clip underneath the structure of the natural systems in order to attempt to convey how non-Euclidean geometry interacts in the real world. Also projected were brain neurons firing over a man ray animation over a paper stagnant structure, commenting on the plastic nature of such perceived structures (like the brain).

The projection in its current form, as I have found, does not generally encourage play-which is particularly unnerving. It was supposed to encourage play on a subliminal, curious, level and encourage the audience to take notice of the mild changes in their perception of natural forms and continue along that axiomatic line of thought. I had in mind the type of play that Non Euclidean geometry calls for: a mental invisible type of play- a play that requires a deep introspection on such systems of thought. This, in retrospect, is a very hard goal to achieve. Nevertheless, I will continue to try. Urbanscreen seems to encourage such introspection quite well, part of me wonders if it has to do with the way sound is used in their constructed environments.
Time constraints definitely hindered my project and resulted in a less than desired result, particularly when it came to the structure. I did not have the time or materials to build out the space as intended, but it was a good lesson when it came to negotiating space and form. This experience will allow me to rely more heavily on the importance of light.
Inspiration
There were some artists that formed and inspired my design and conception. Feng Mengbo, with Long March: Restart (2008,) created a narrative of his life during Mao’s regime utilizing the structural elements of a Mario video game. With no context, the user does not know he is playing in a complicit power structure but still embeds the basic motivations, goals, and necessities of the characters of that time.
Nalini Malani’s Gamepieces (2003/2009) works with how components of her work adapt to the architecture of space, which directly results in works success. Actively juxtaposing images of war and violence, blue skies, and “earthly images” project from the mobile, cylindrical structures in Gamepieces. Malani’s “comment emphasizes contingency. In the hierarchy of components that constitute an artwork, it seems obvious to emphasize the importance of the constant non-varying components.” (Gamepieces: An Installation Deconstructed, Briggs, Sydney, 2015). Nalini Malani plays on the audiences want for a presupposed hierarchical structure of components and allows the removal of such hierarchical systems to allow the audience to reflect on that.
Kara Walker relies on the historical system of adding meaning to eighteenth-century cut-paper silhouette to critique historical narratives of slavery in “Gone: An Historical Romance of a Civil war as it Occurred b’tween the Dusky Thighs of One Young Negress and Her Heart” (1994). Walker juxtaposes tumultuous, unnerving imagery which “confounds conventional attributions of power and oppression” paired with a material derived from a systematic practice of self reference and leisure for white, upper class, people of the south in the eighteenth century- a practice still in place in the south today. Walker relies on the audiences inference on such systems of exploring the self in relation to narrative environment in order to realize how “whiteness is just as artificial a construct as blackness is.” (Walker, Gallery label from Contemporary Art from the Collection, June 30, 2010- September 12,2011, Moma.) The Urbanscreen collective has been a tireless source of inspiration for me while learning about digital media.

The URBANSCREEN collective artistically manipulates the material of light for site-specific public media such as “architectural projections, augmented sculptures, media facade concepts and virtual theatre.” They “investigate the phenomena that occur when the material world is superimposed with the digital, and inversely, when the digital overlaps with reality”. They go on to state “by experimenting with the syntheses of digital media and material objects and spaces, we discover new forms of artistically conveyed studies of a living environment that keeps changing as we speak.” (Urbanscreen, 2015) Urbanscreen looks to working with a new living environment in order to augment our perceptions of what a proper reality looks like, which opens the door to many unknown effects: culturally, cognitively, and artistically. All of which constantly interplay and negotiate with each other to create our shared reality.