I struggled with grasping the essence of Nees.
As much as I appreciated his infamous falling squares, I did not intend to simply tweak his works. Yet I wasn’t able to conceive an interesting generation that capture the same spirit yet is totally original… Thus was my dilemma. Thankfully, my comprehension of Stochasticism evolved as I tinkered with a variety of ideas.
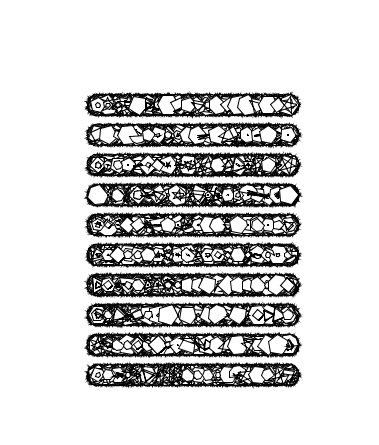
During my first effort, I scanned through a series of works both by renowned artists and my classmates to gain inspiration. From the examinations I realized that despite the wide range of complexities, all of their works had the basic shapes to serve as the base camps (circles, triangles, squares, lines, dots). I immediately felt the urge to operate with something different: polygons. To add some flavors, I decided to grant my computer the power to choose how many sides the polygons had each time around the loop.
Since polygons are relatively difficult to draw, I created a separate function called void poly(float r), where r pin-points the total number of sides. I used float by mistake, but then to my surprise, the program ran smoothly without crashing. This was a mystery since theoretically, non-integer sided polygons can not exist. Within the draw() function I randomized r to achieve the effect I intended. After playing around with the polygonal techniques, I applied two for-loops to create a straightforward array (image below).
I experimented with the different parameters such as sizes, spacings, to generate my work(s) -(the upper-most two images). I observed during my trail and error process that, resetting the background within draw() made a significant difference in the collective progression of the arrays. An example would be the apparent visual contrast as well as difference in affect of the two images, even though only one condition was adjusted.
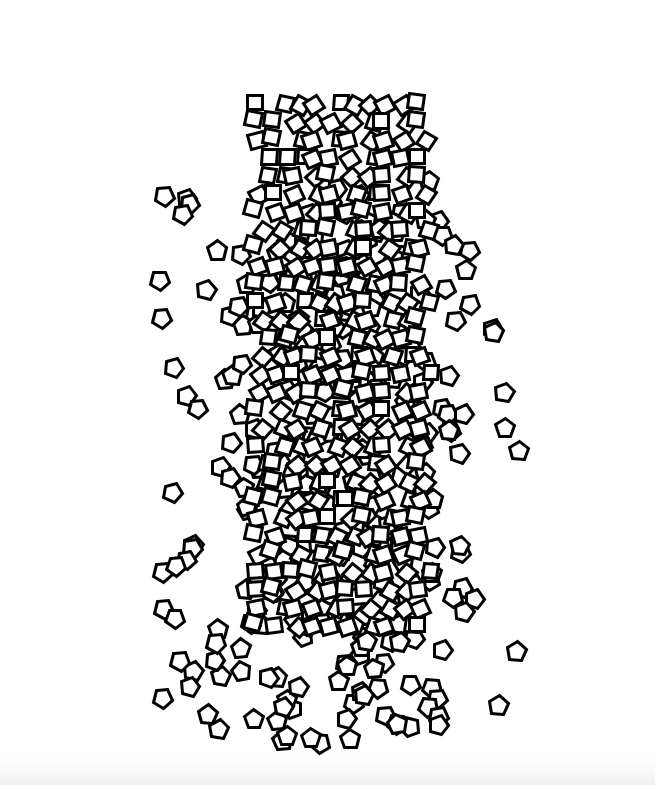
The second attempt was the most Nees – like. This time I built upon Georg Nees’ Schotter idea.
Instead of having one progression going on, I tried having two separate yet spatially overlapping progressions in play. The outcome was satisfying. The canvas starts with an array of squares stacking over an array of pentagons. Soon after, the squares begin trembling, whilst the pentagons jump around and get way too excited. Strangely, it reminds me of juggling, or a crowd cheering over a triumphant hero. The effect originates from the fact that pentagons translate and rotate at a faster pace than the squares.
During this ‘enjoyable’ process, I came to a vital realization: unexpected beauty can often arise from randomness under control. Too much structure appears stiff and boring; over-indulgence in randomness yields to chaos, which is also reduced in aesthetic values. The interplay between randomness and structure is a tricky territory. It takes a dose of courage for the artist to surrender a portion of the control, and the entrusting computer to finish the job. To the artist’s delight, the computer rarely disappoints.