

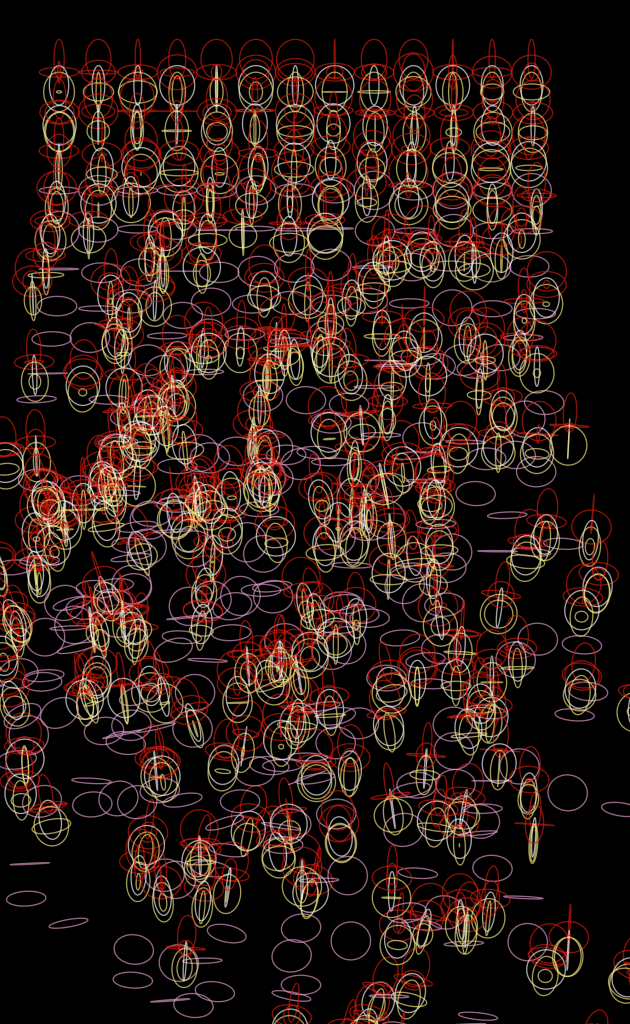
When examining Georg Nees’s work, I became perplexed with his ability to seamlessly alter his structures using ‘randomization.’ I love the thought of messing with set, orderly structures, however, I am usually a bit afraid to randomize aspects of my work. It is clear through Nees’s work that although there is an emphasis on the randomization, it does not necessarily have to be an abrupt transition. With this in mind, I decided to begin working on my first iteration for my series.
When altering all of my sketches for this series, I did not have a set final product in mind, rather, I wanted to randomize different aspects of my code and see what would happen. I felt that by working in this manner I was able to more accurately understand Nees’s process while he was creating works like Schotter (1968). I set a few parameters for myself: such as making sure I kept a grid present at the beginning, using ellipses as my main shape, and to inject a sufficient amount of color.
At first, I randomized different aspects of my translation function as a way of tweaking the intensity of the randomness. I loved how the chaos slowly erupted towards the bottom of the frame, however, I was a bit bored with just one set of ellipse cells on the page, which prompted me to add multiple layers of ellipses inside of Push and Pop matrices. After I achieved a dense layering effect, I decided to make the background black and changed each one of the Push/Pop matrices’ strokes to varying colors that I chose at random. I am aware that although this is my first iteration, it is a tad chaotic which is a little bit off-kilter for Nees, however, I wanted my end product to be disorienting and full of randomized functions, so I feel that this is relatively tame compared to the rest of my series.
Moving forward, I wanted to throw off the modularity of the ellipses. The first change I made in my second iteration was to randomize different aspects of the cell size within the individual ellipses inside of the push/pop matrices. In doing so, I was able to alter the width and height of a few of the cells at random, which is meant to both confuse and draw in the viewer. I also wanted the chaos to start earlier down the line in the grid, so I doubled the random value in the translation function to achieve that. I really enjoyed the effect that that gave off, as the ellipses began to flutter off in different directions, almost as if they were independent organisms.
In my final iteration, I wanted to completely transform the sketch with just a few subtle tweaks. I started by adding a few more push/pop matrices, and randomized the width and height of all of the ellipses. Ellipses of all different shapes and sizes were strewn across the canvas; it looked as though they had erupted from the center. I randomized the strokes on a handful of the ellipses just to keep another level of chaos alive. To complete my process of disorienting the viewer, I multiplied the random value in the translation function by ten. The combination of adding push/pop matrices, randomizing the width and height of the ellipses, and increasing the value that the random value is multiplied by emitted a fiery, chaotic final piece for my series.
All in all, I really enjoyed using Nees’s recipe for creating a randomized series. Starting off with the standardized ellipse grid, I slowly allowed for the computer to take control by randomizing select aspects of my code. I feel like the transformation from my first to my third piece is clear but not too abrupt–one can tell that there has been a lot of changes but I hope that it is not too polarizing. I think that in following in Nees’s steps, I learned a really valuable lesson in letting go of my preconceived vision for my work and to appreciate what the program has to offer!

